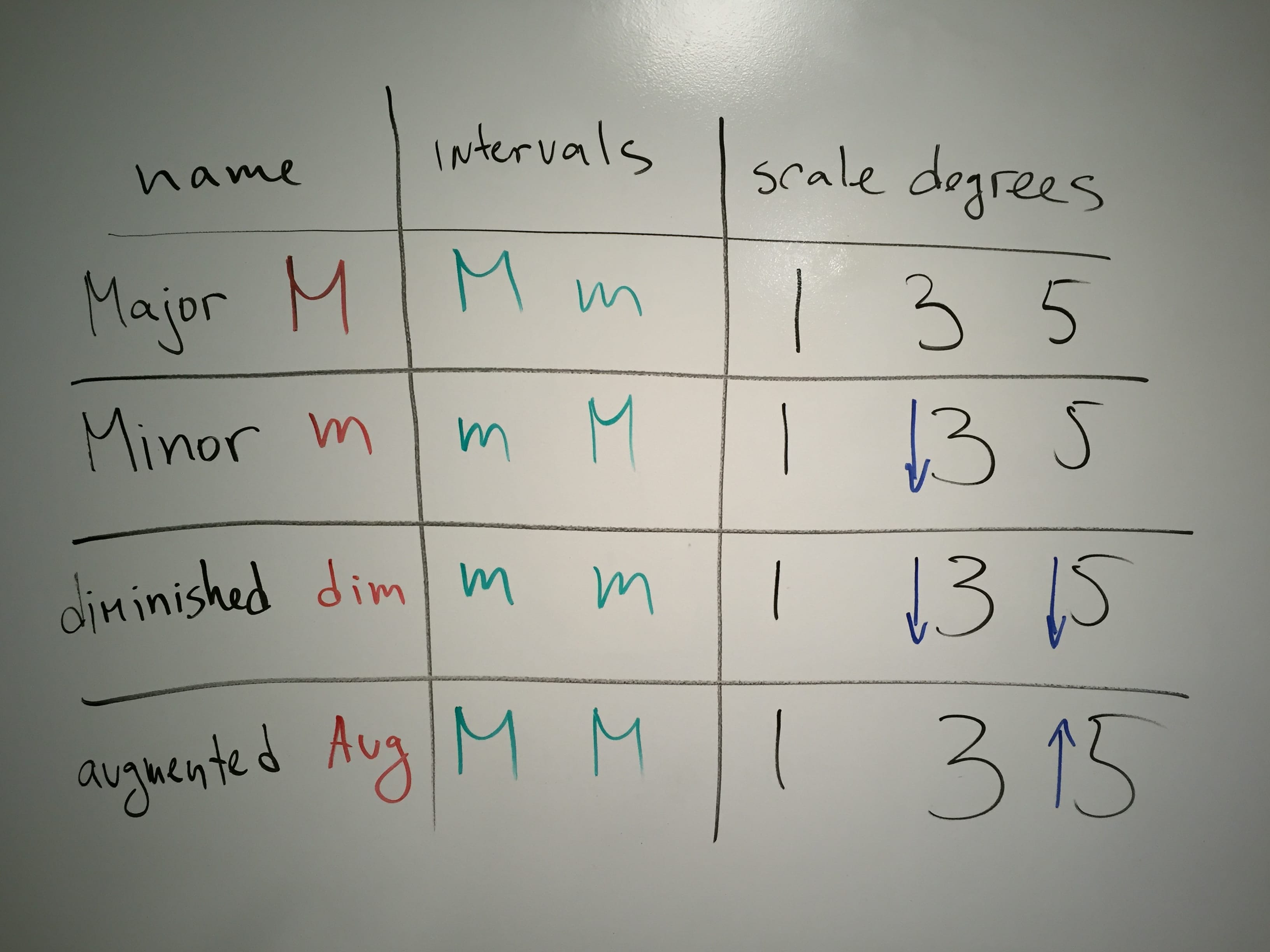
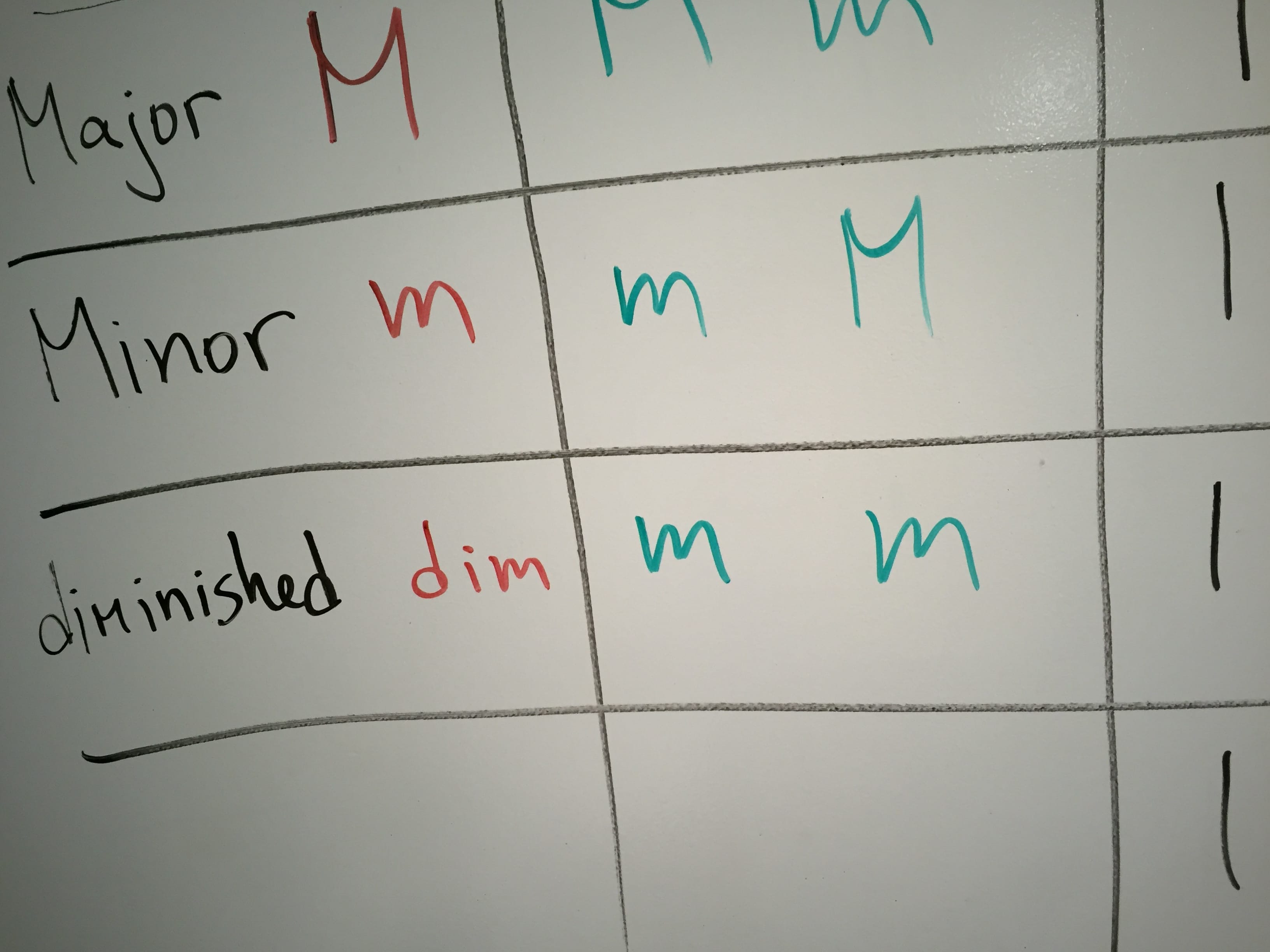
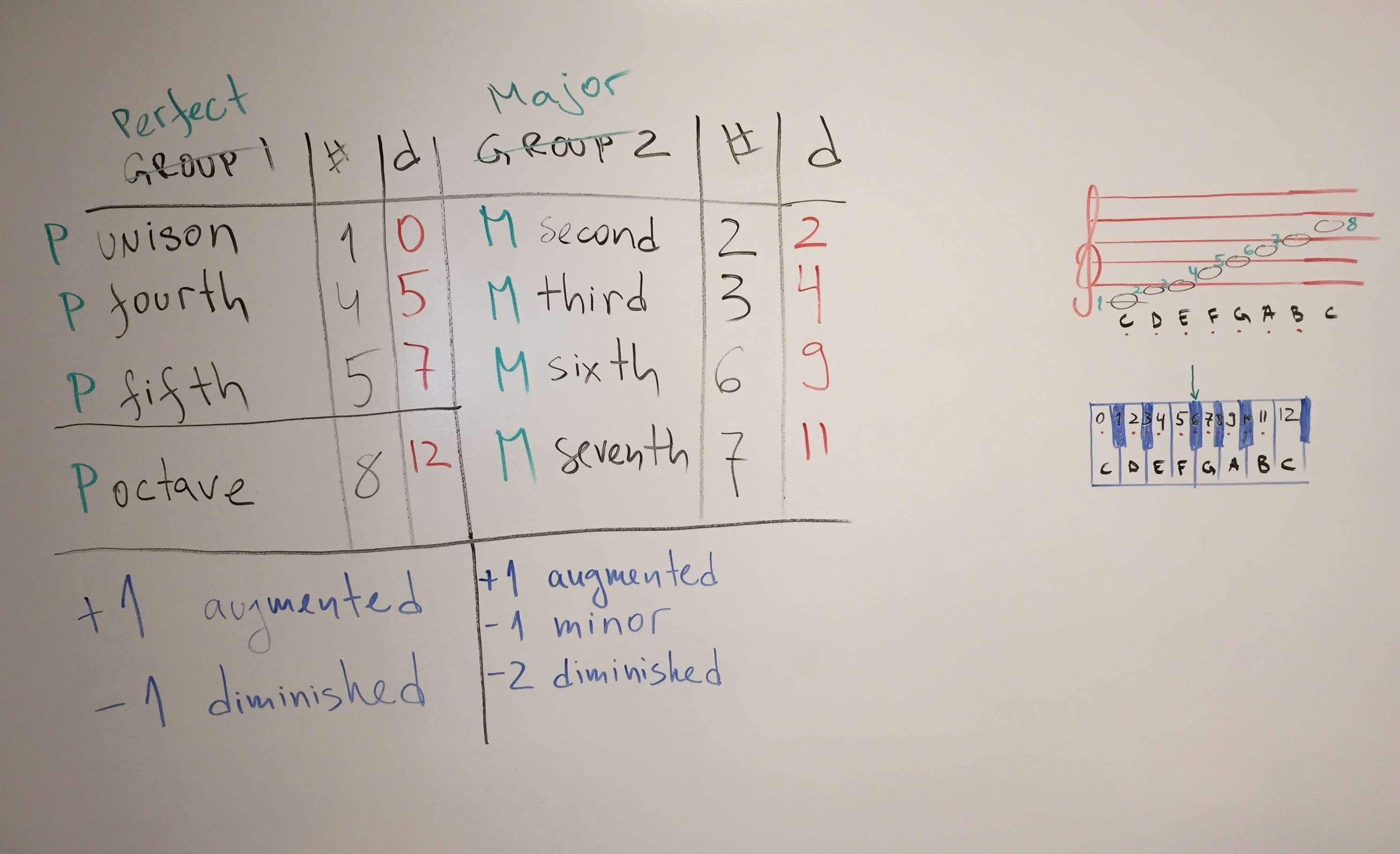
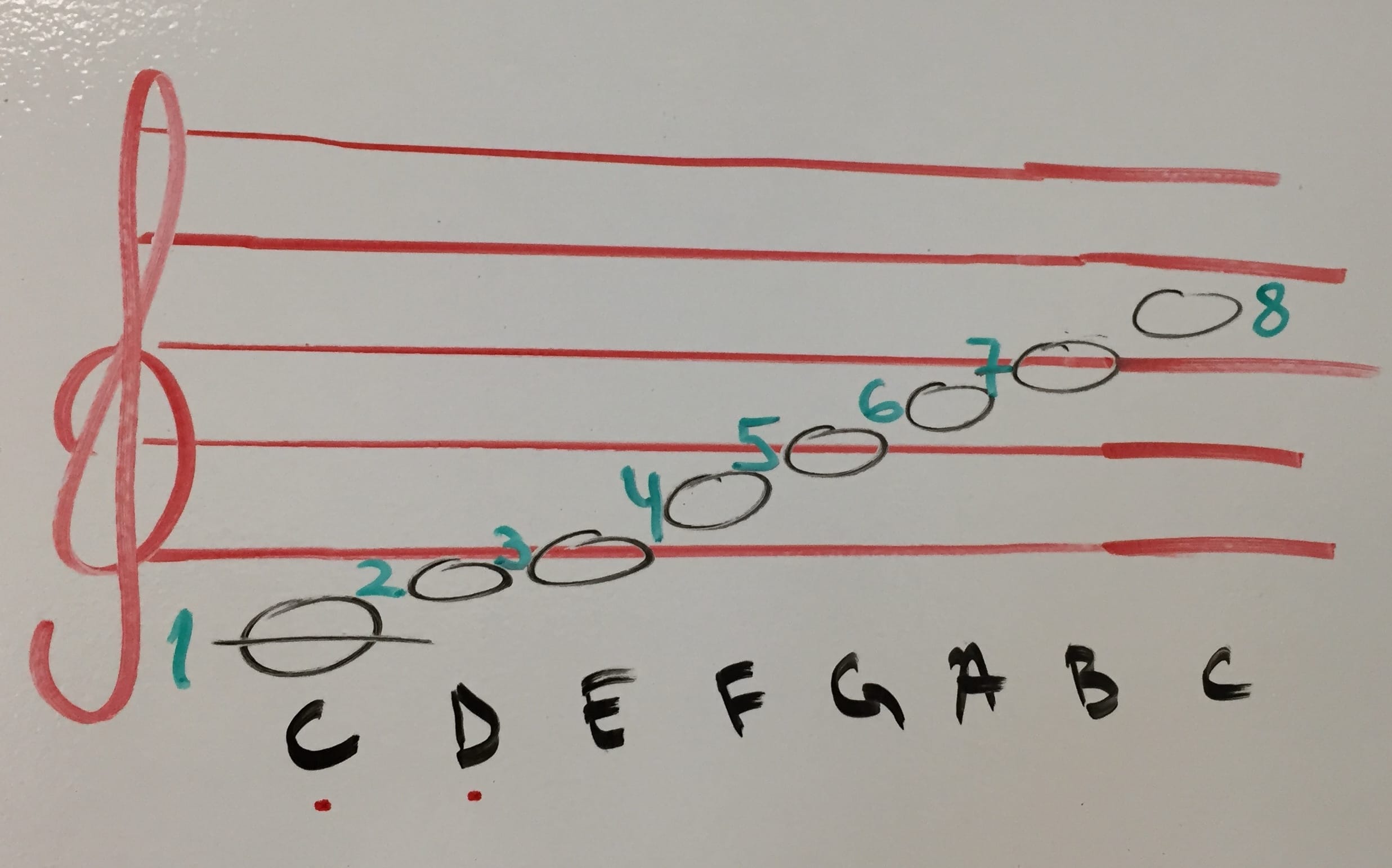
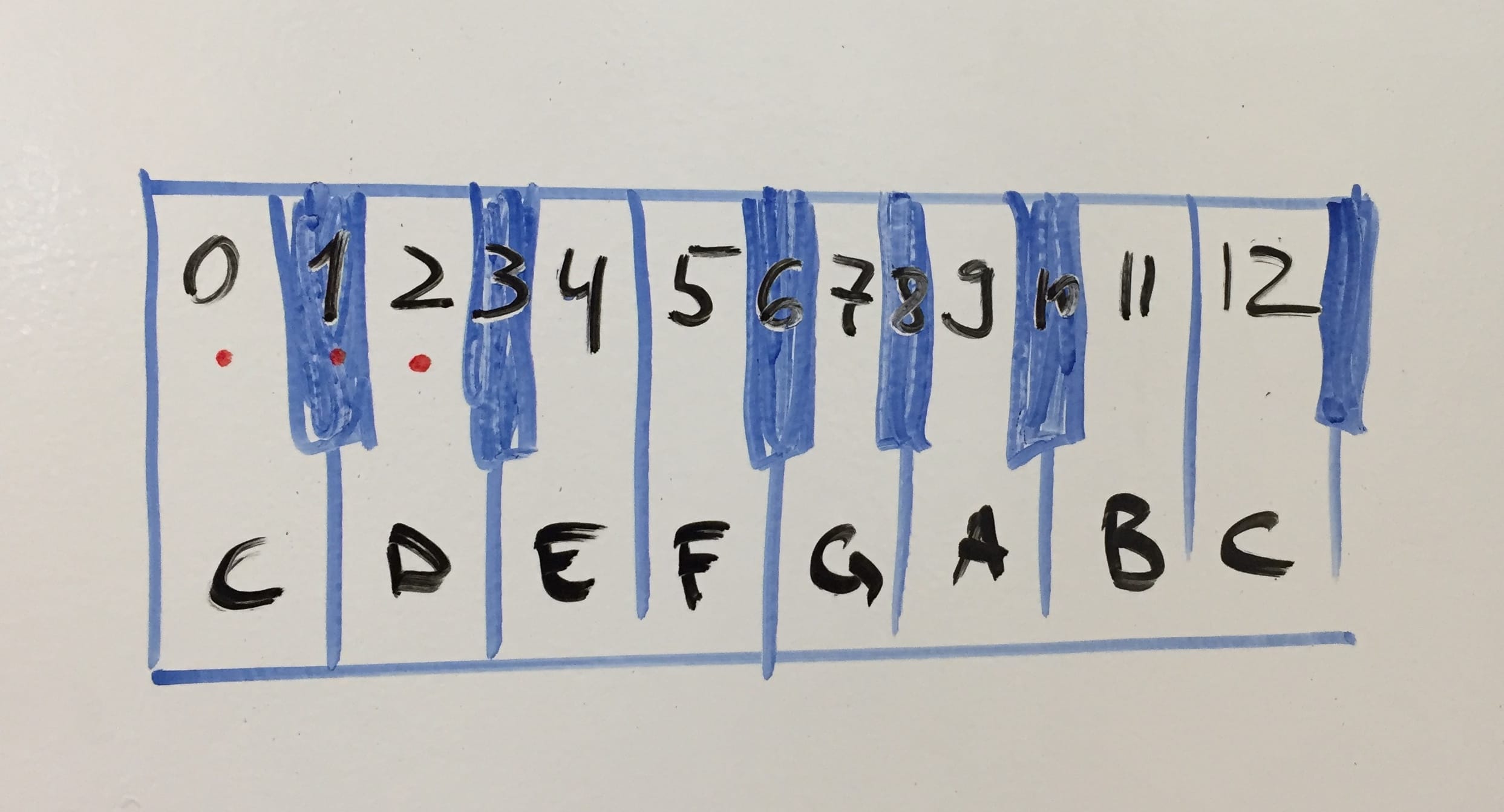
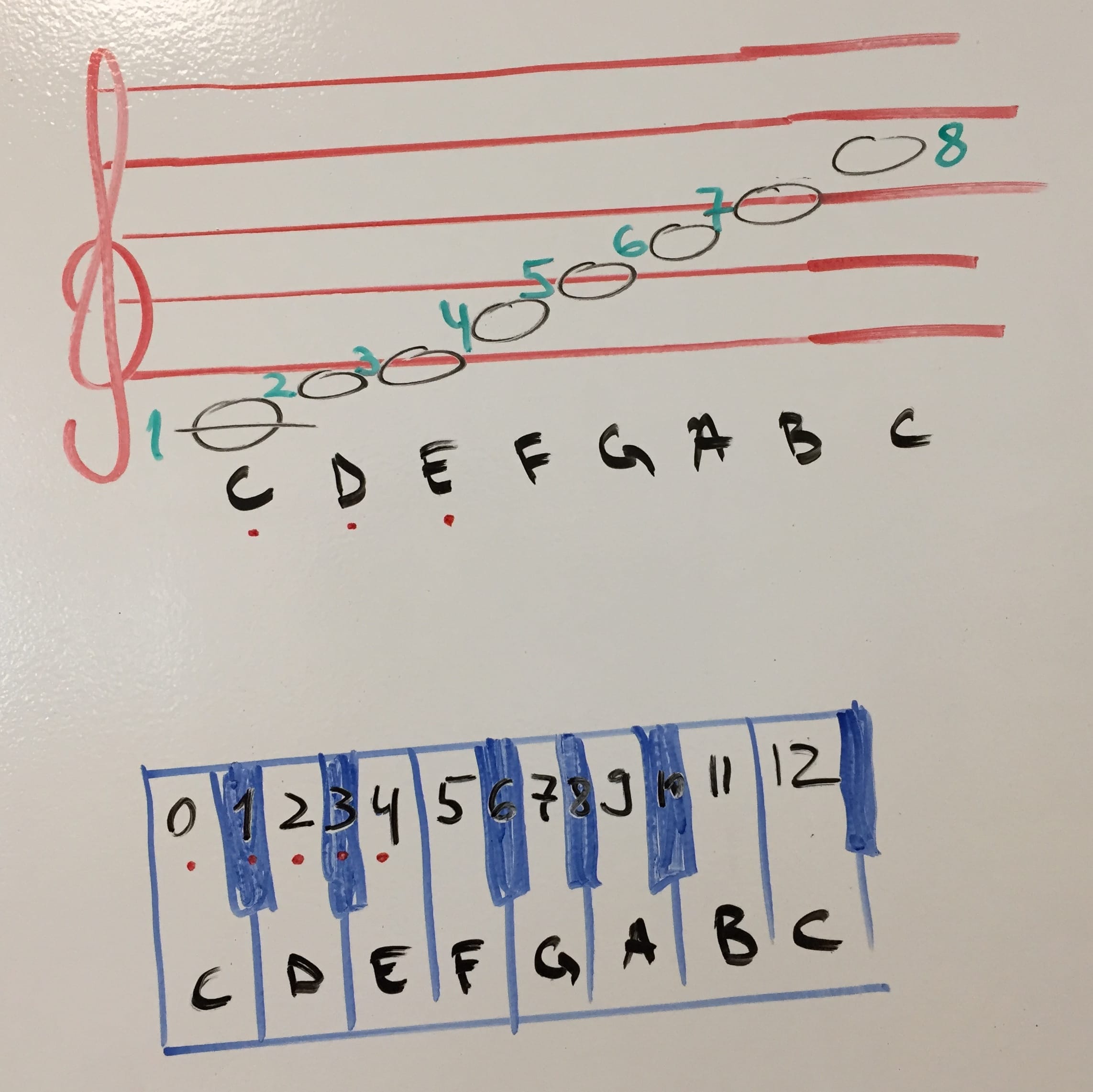
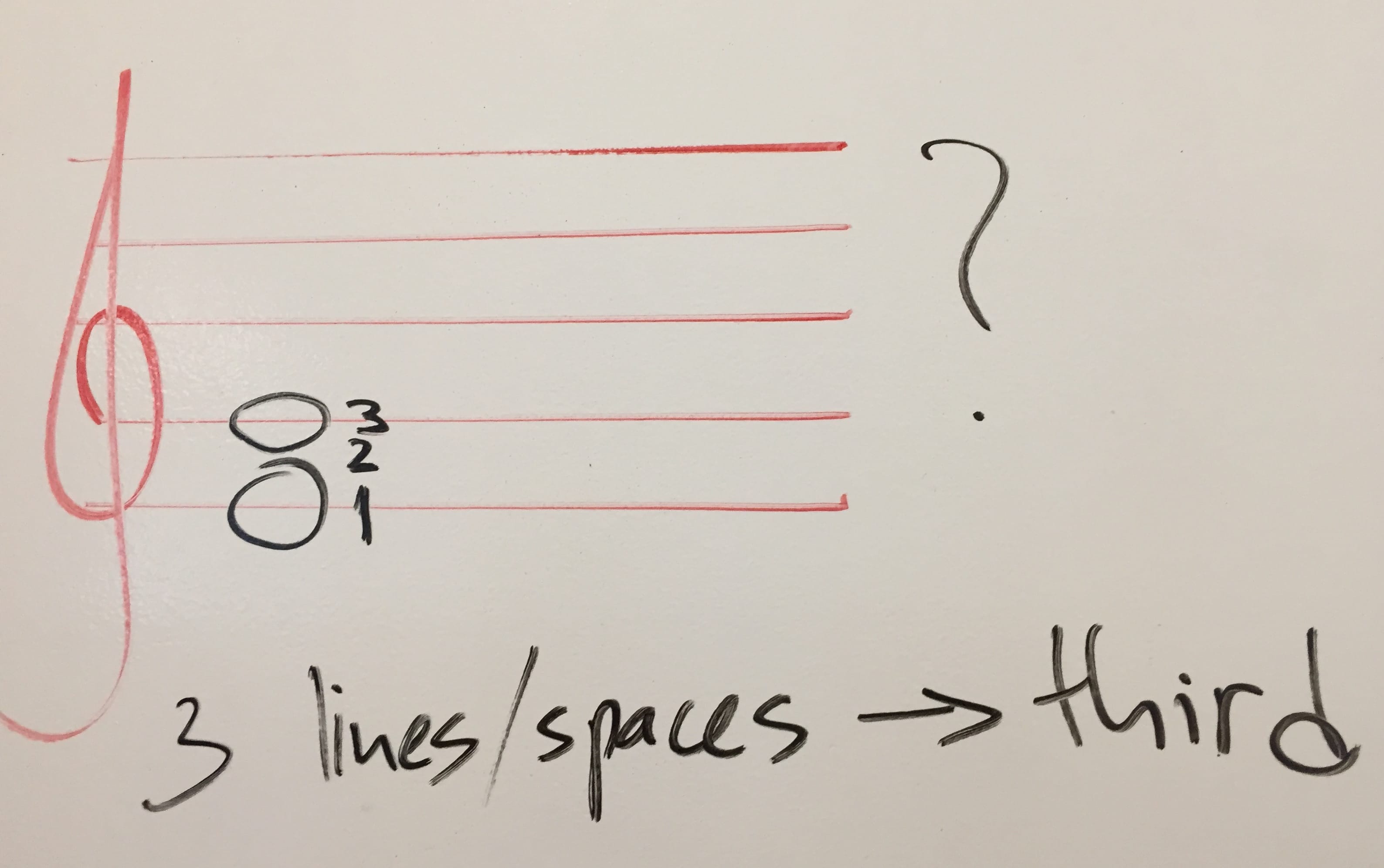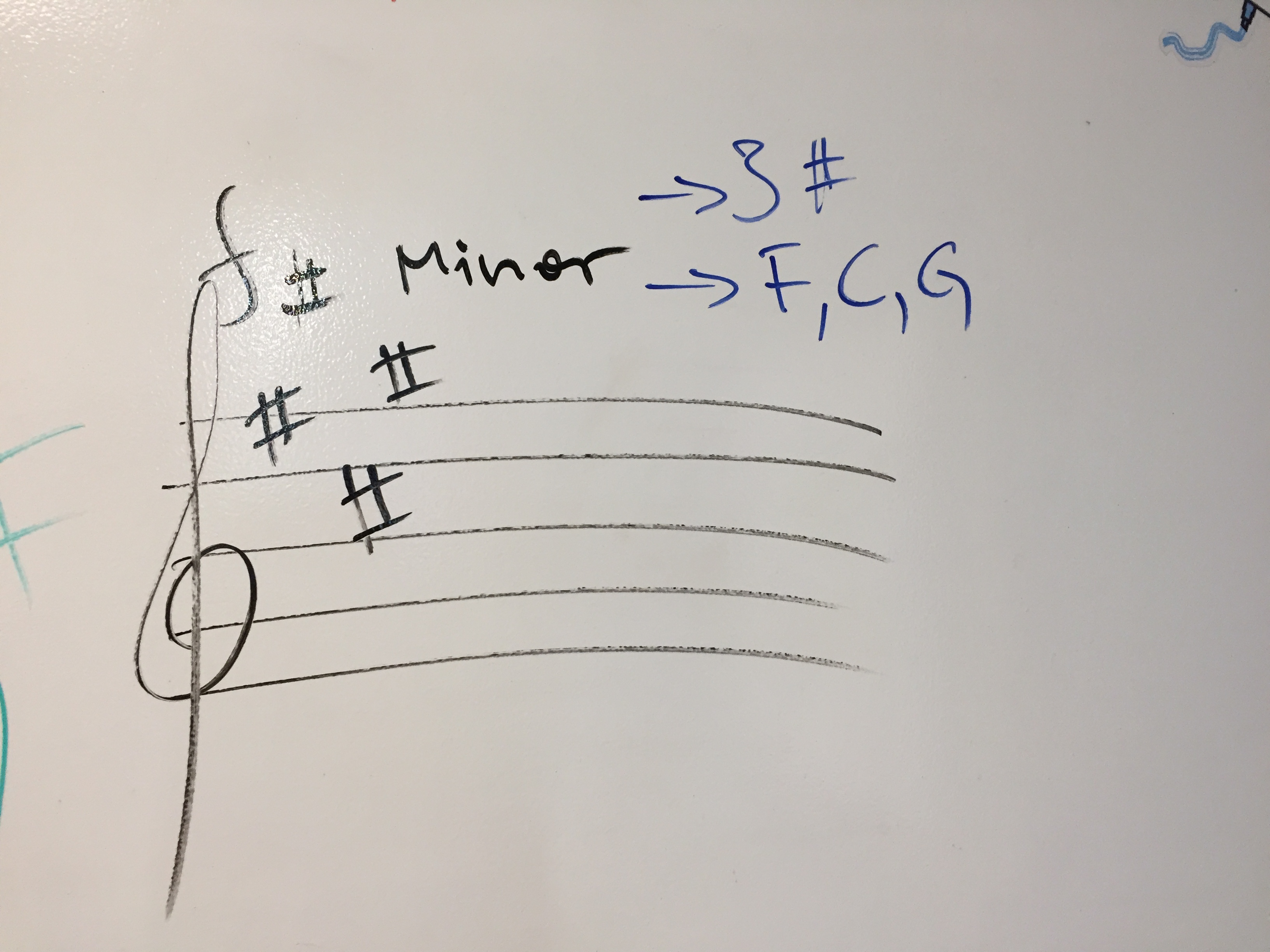People are fascinating creatures. We can perceive differences in air pressure as pitch (sound, tone). Provided that said changes in pressure are fast enough and cyclical enough. OK, some clarification…
Wave your finger. No sound. Now faster, faster. If you manage 20 times in a second, you’ll start hearing something. 20 times-per-second is also measured as 20Hz. 20 000 times-per-second is 20 000 Hz. Or 20kHz. This (20Hz-20kHz) is the range of human hearing, at best. As we get older, the top falls down to 18kHz, 17kHz… Dogs do 50kHz. Bats – 100kHz.
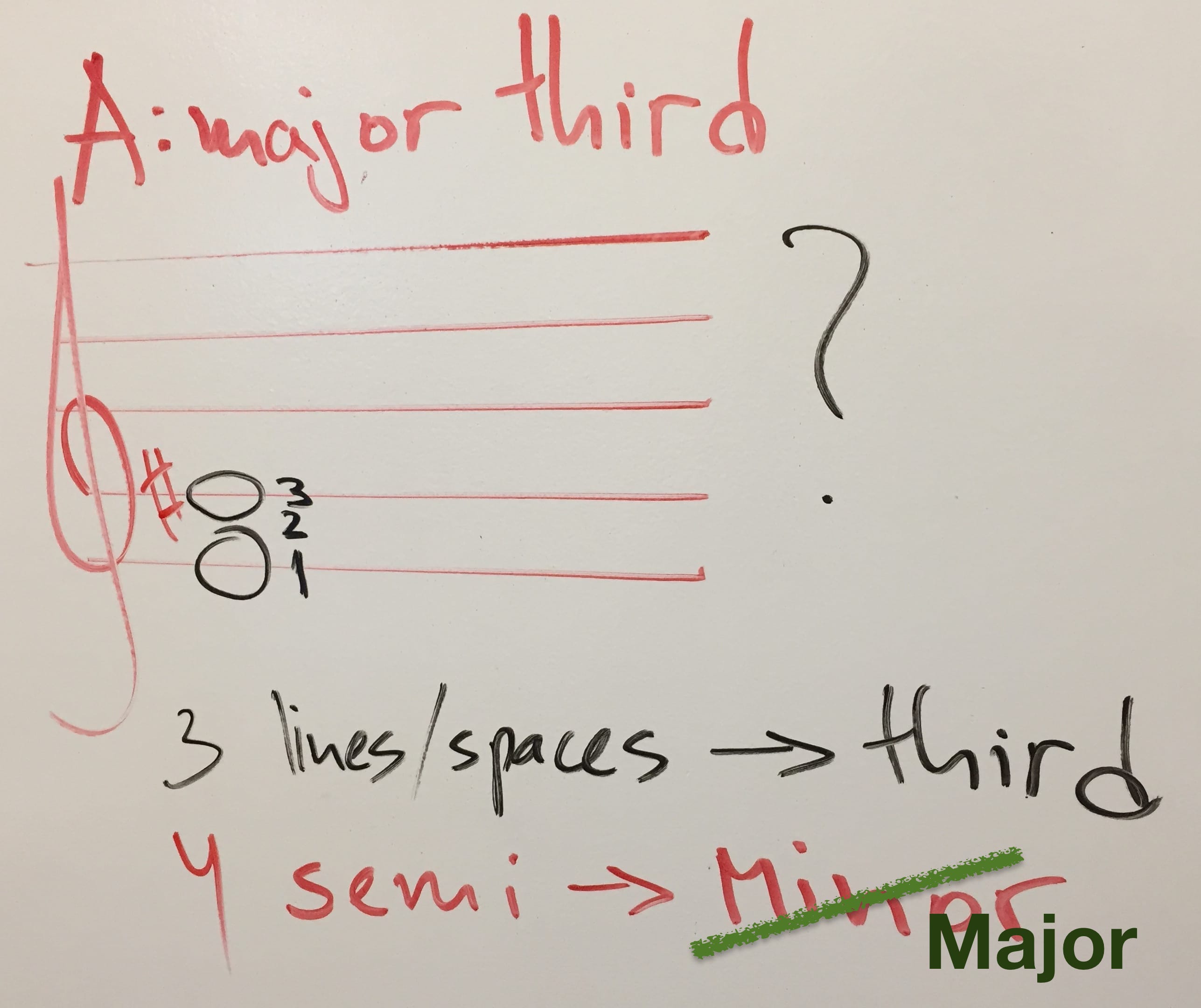
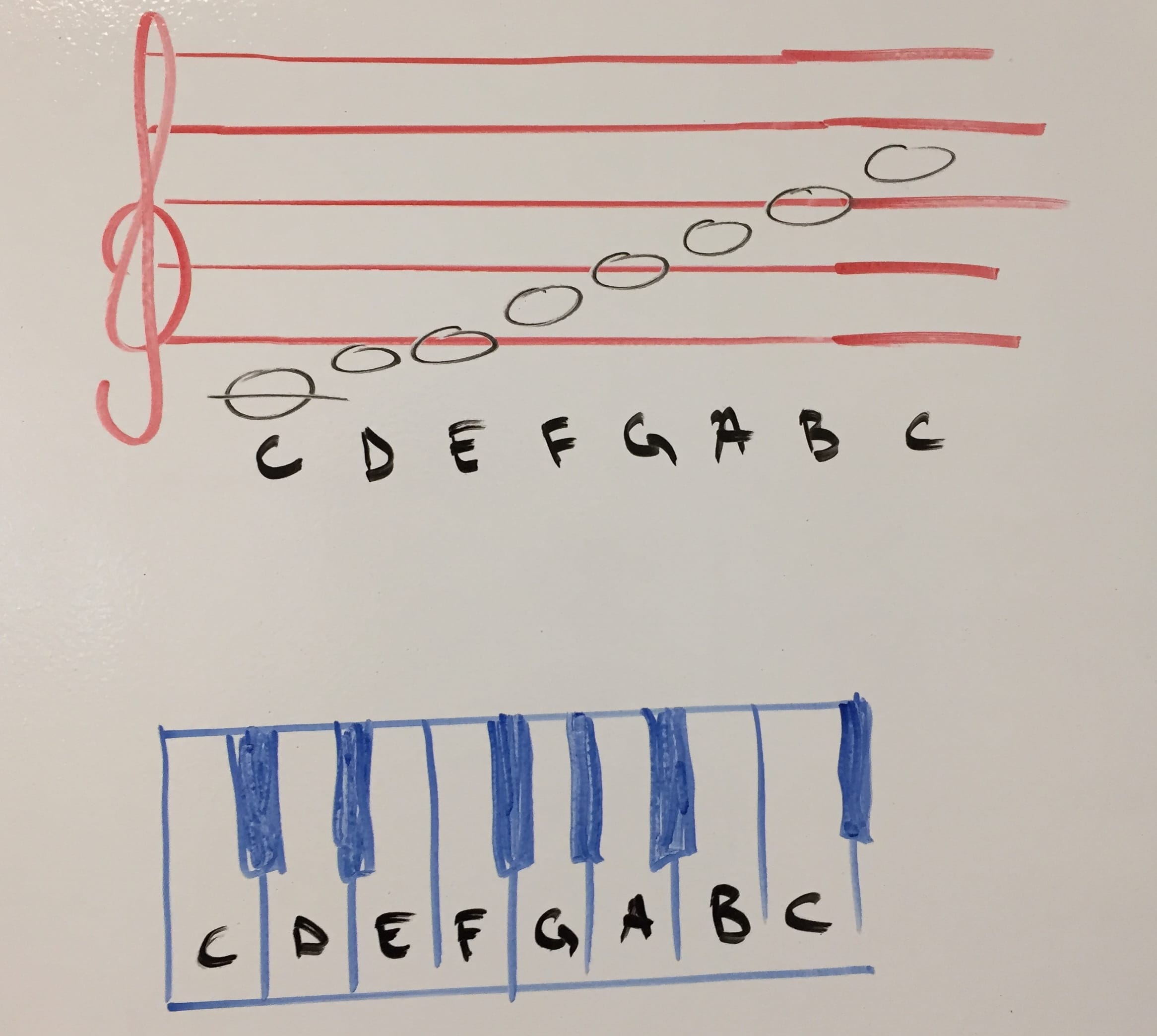
So we perceive this quick change of low-to-high-pressure-and-back as pitch. For example 55Hz is the note A.
How can you tell when this 55Hz note A is played by a guitar or a piano? It’s the same frequency, no? Well, the thing is that nothing in nature is perfect and there’s no 55Hz-only waves produced by instruments. In addition to 55Hz a piano string also vibrates at 110Hz (double the frequency), at 165Hz, at 220Hz… etc. All multiples of 55.
We say that 55Hz is the fundamental and additional frequencies are overtones. They are quieter and different in intensity for different instruments. That’s how we can tell a violin A – based on its overtones (aka timbre).
Now, this is all cool. But the point of this post is to show that we don’t even need the fundamental. And we’re able to tell the “base”, fundamental pitch, even when it’ missing! What wizardry is this!? Demo time!
Poof! Proof!
Let’s see an illustration using the Reaper software.
Sine wave
Create a sine wave at 110Hz which is A2 – the second A under middle C (C4).

It’s just a simple wave, not pleasant to listen to at all. It sounds like nothing in the real world, no overtones are present, just a fundamental. This is what is sounds like:
Now look at the result using the free SPAN frequency analyzer. As expected, there’s the bump at 110Hz and mostly nothing else.

Now let’s insert a precise EQ between the sine wave and the analyzer and cut off everything under around 300Hz.

As you’d expect after we’ve cut off most all of the fundamental frequency, there’s nothing left. No sound. (To be fair if you turn all kinds of gain, you’ll hear something above 300Hz because the sine wave still has some energy, see the EQ screenshot, but it’s so faint it’s not even there)

Let’s hear the audio. A sine wave at 110Hz:
And after the EQ at 330-ish Hz:
(Yup, it’s almost complete silence)
A2 sample
Now let’s try the same but with the sound of a sampled piano with the same note A2.
Here’s what it sounds like:
And here is what it looks like in a frequency analyser:

As you can see, in addition to the fundamental at 110Hz, there are overtones, all multiples of 110. First one is at 220Hz, this in A3, meaning an A an octave higher than the fundamental. There’s another A at 440Hz, another at 880Hz and so on… but there’s more than As going up in octaves. At 330Hz that’s an E. At 550Hz that’s a C#. A, C# and E spell a nice A major chord. 660 is another E, cool. 770 is G. OK, this is A major seventh. I can live with this. 990 though is a B. Damn, now we’re getting jazzier and jazzier with these chords. The thing is these overtones are quieter and quieter and we do not perceive a chord, but just a single pitch A2. Although there’s a lot more going on. What exactly is going on is dependent on the instrument (thimbre).
Aaaanyway.
The interesting thing is what happens after we insert the same EQ and cut off all below 300Hz. Meaning we’re killing the 110Hz fundamental. And even the first (strongest) 220Hz overtone.

What do you think is going to happen? Listen:
Before:
After:
What?! Sounds a bit different, more telephony maybe. But we still perceive the same note. The same tone. The same A2. We’re missing the most important information (110Hz) and second-most important (220Hz) but we still hear A2. On a piano. Solely based on the overtone signature of this sound.
Dunno about you, but I am amazed by this.
Just one more: A3
A3 piano sample. Before EQ:

After the same 300-ish Hz EQ:

Listen…
Before:
After:
We still perceive the same A3 (220Hz) even when there’s nothing there!
So what?
Well, it’s a fascinating phenomenon if you ask me.
Also one of the things when producing music is you often want things (voices, instruments) to be audible and distinct. When there’s too much information in the same frequency area, sounds get muddy and hard to separate by the listener. That’s why there’s often a lot of cutting out of frequencies to make room for other instruments. This example here shows that if you need to, you can cut even below the fundamental frequency of the note being played and we humans can still tell the note. Weird. But true.