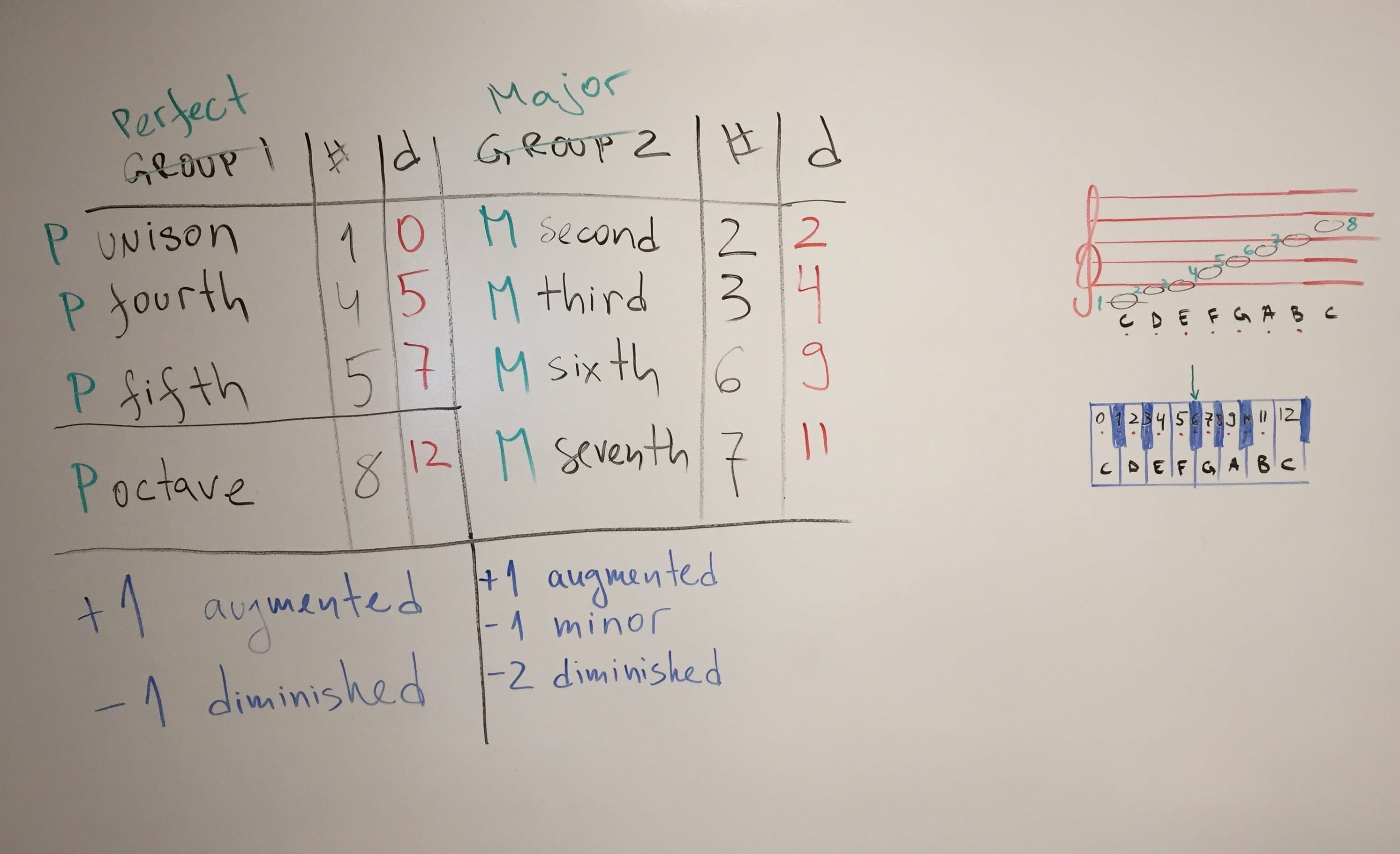
In the previous installment you learnt how to draw this table of intervals:

Now let’s figure out how to use it and also finish it up until it looks something like:
OK, let’s start by figuring what in the world is this interval supposed to be:
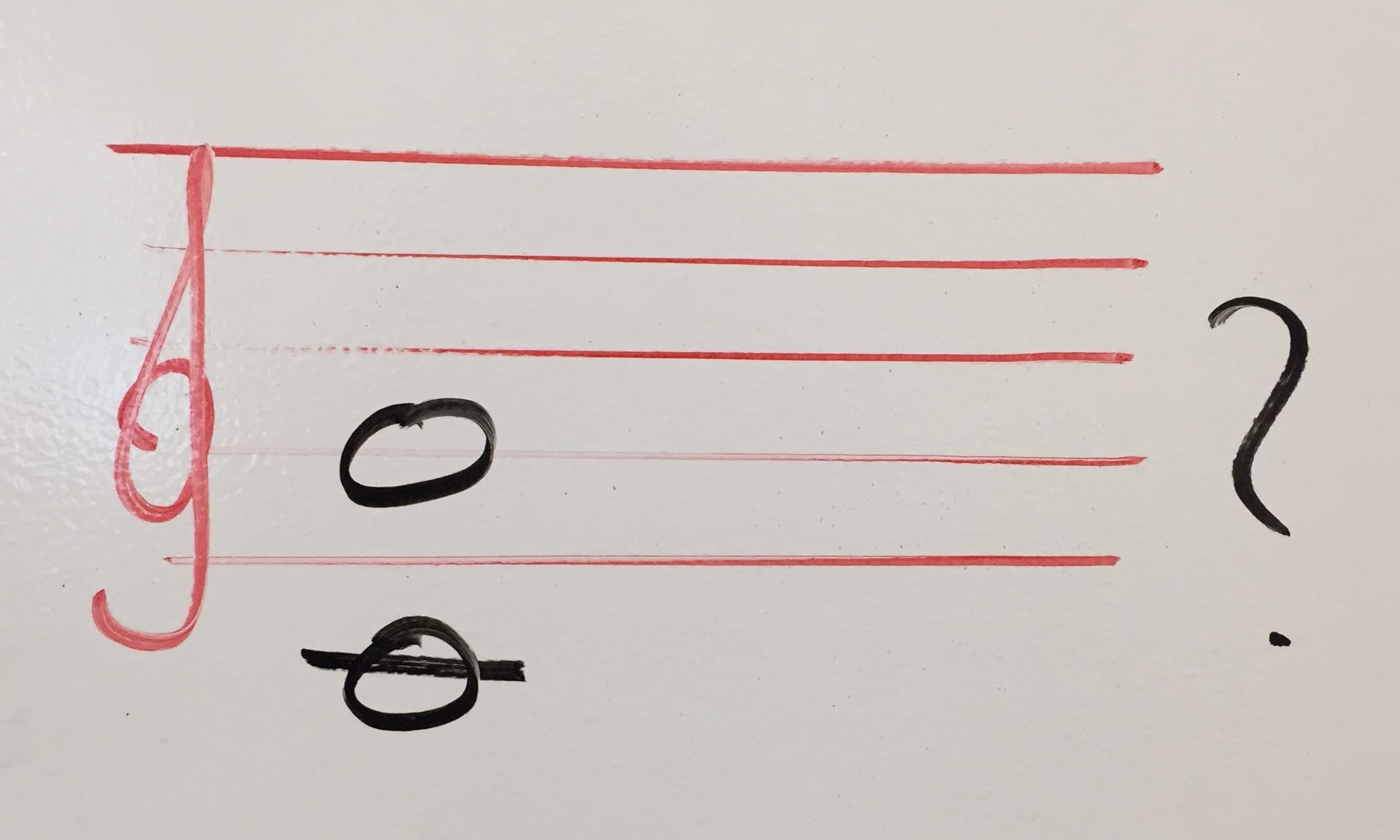
This is C and G. Let’s count the number of lines and spaces, starting with the initial note.

There are 5 lines and spaces. Same if you use the alphabet ABCDEFG and count C = 1, D = 2, E, F, G = 5.
You can also use the little helper tool and note the number next to G.
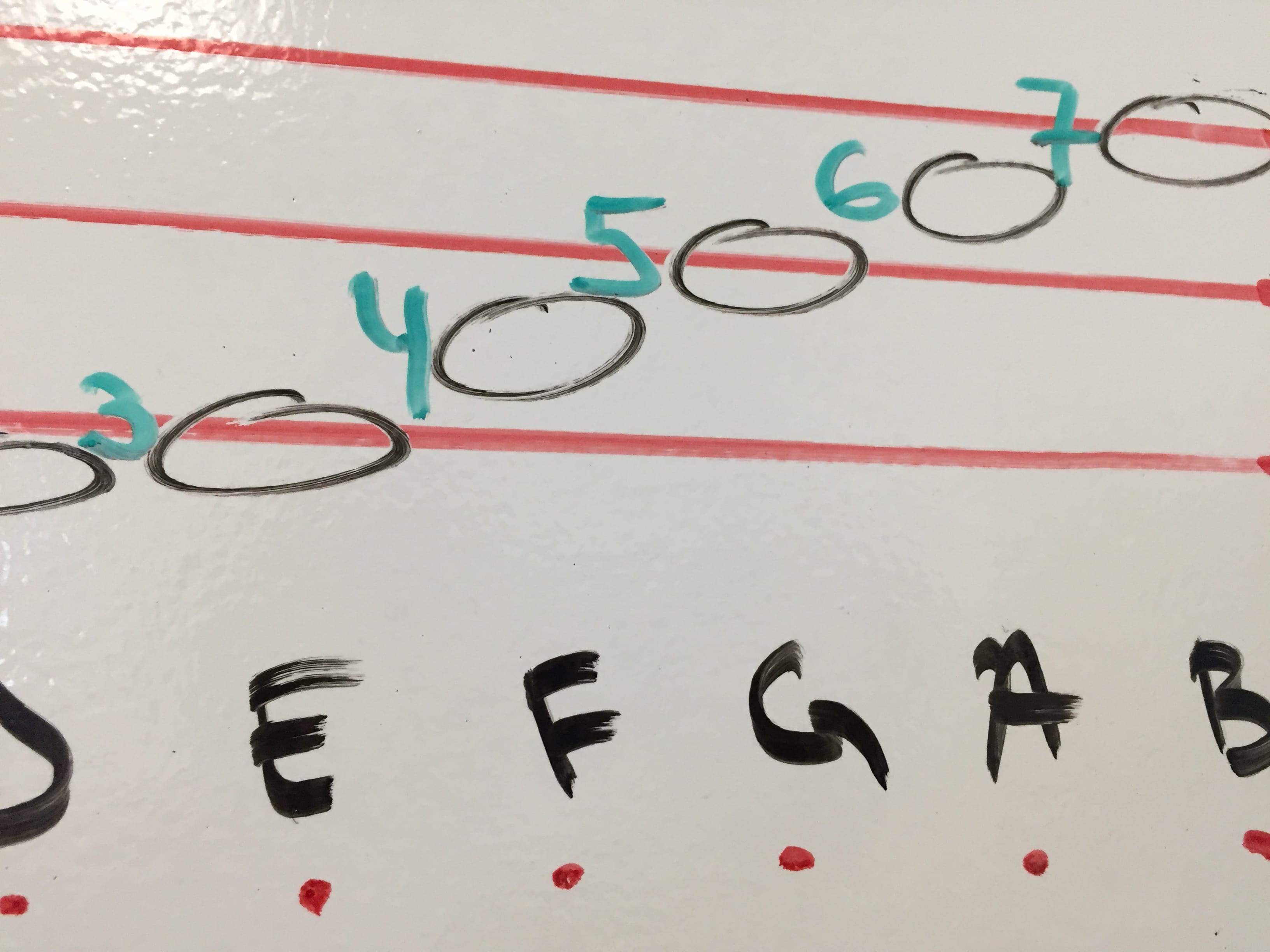
At this point we’re pretty clear these are five lines and spaces. Write it down.
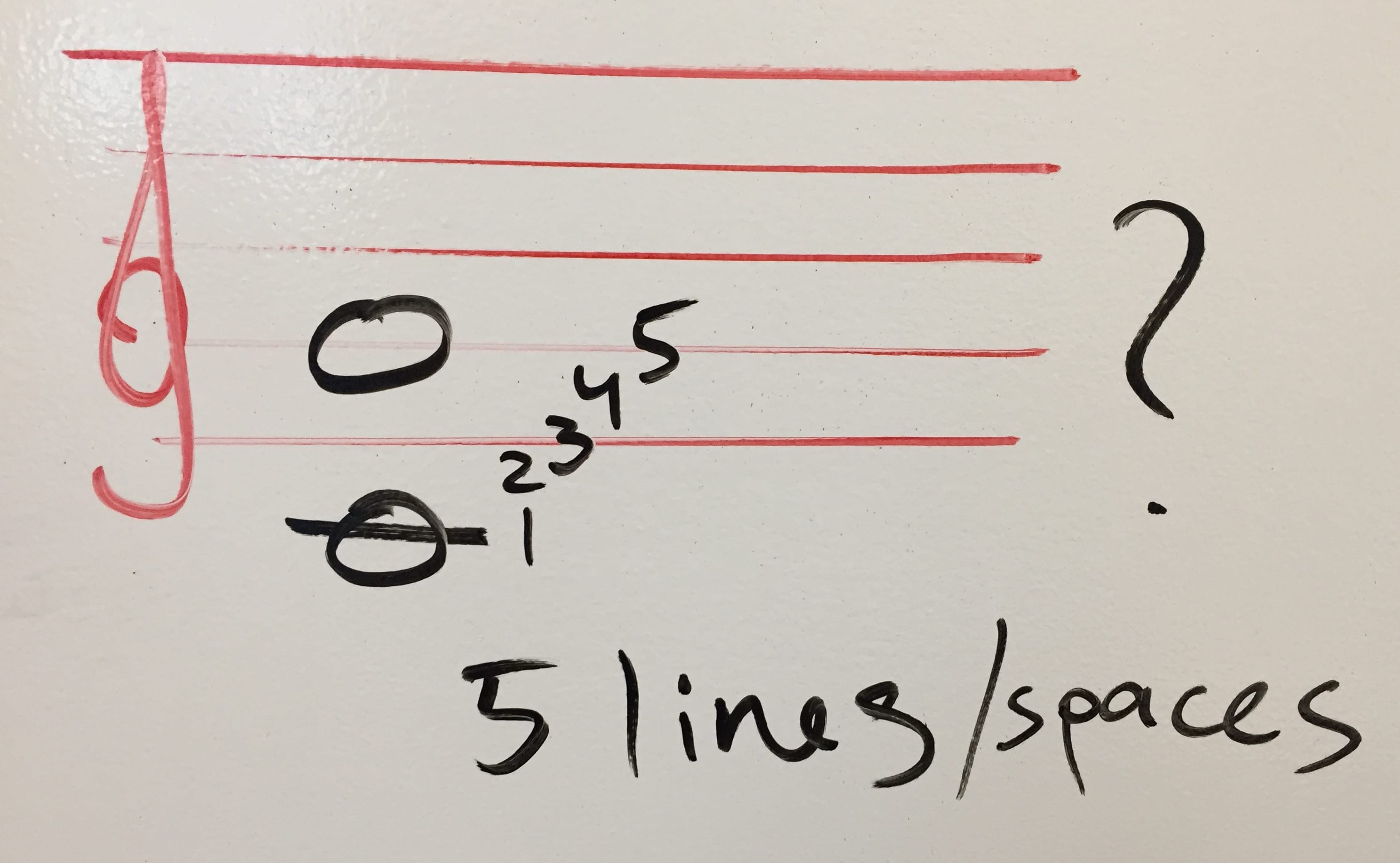
Now you need to count how many semitones are between C and G. Using your keyboard, put your finger on C and count every time you move. You end up counting to 7.

So 5 lines/spaces and 7 semitones.
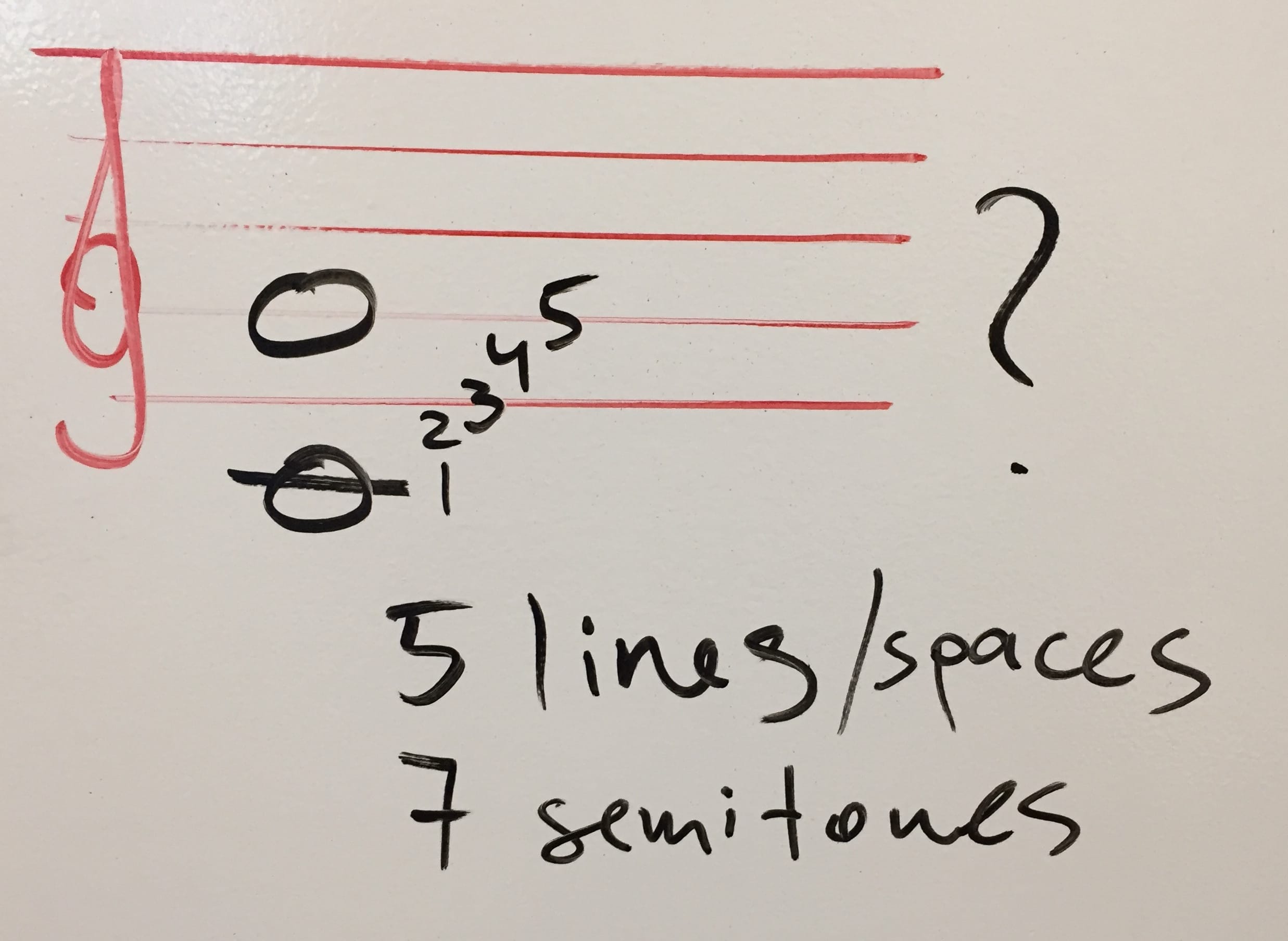
Time to look at the table of intervals. You find a row that says 5 (# lines/spaces) and 7 (distance in semitones). We have a match!

Therefore you conclude that the interval C to G is a perfect fifth. Success!

Now what if you have G♯ instead of G. What do you call the interval between C and G♯? G♯ is still on the same line. So the number of lines and spaces is still 5.

But what about the semitone distance?

Using the keyboard to count you end up with 8.

But in the table we don’t have 8. We have 7.

The interval is no longer perfect, because it was augmented with 1. Hm, what do we call it? Here’s an idea – we call it augmented fifth.
In conclusion, the interval between C and G♯ is called augmented fifth.

Now what if you have G♭ instead of G? Same 5 lines of spaces but different semitone number.

Using the keyboard and counting, you get to 6. (Starting from and skipping C, you have C♯ = 1, D = 2, D♯ = 3, E = 4, F = 5, G♭ = 6).
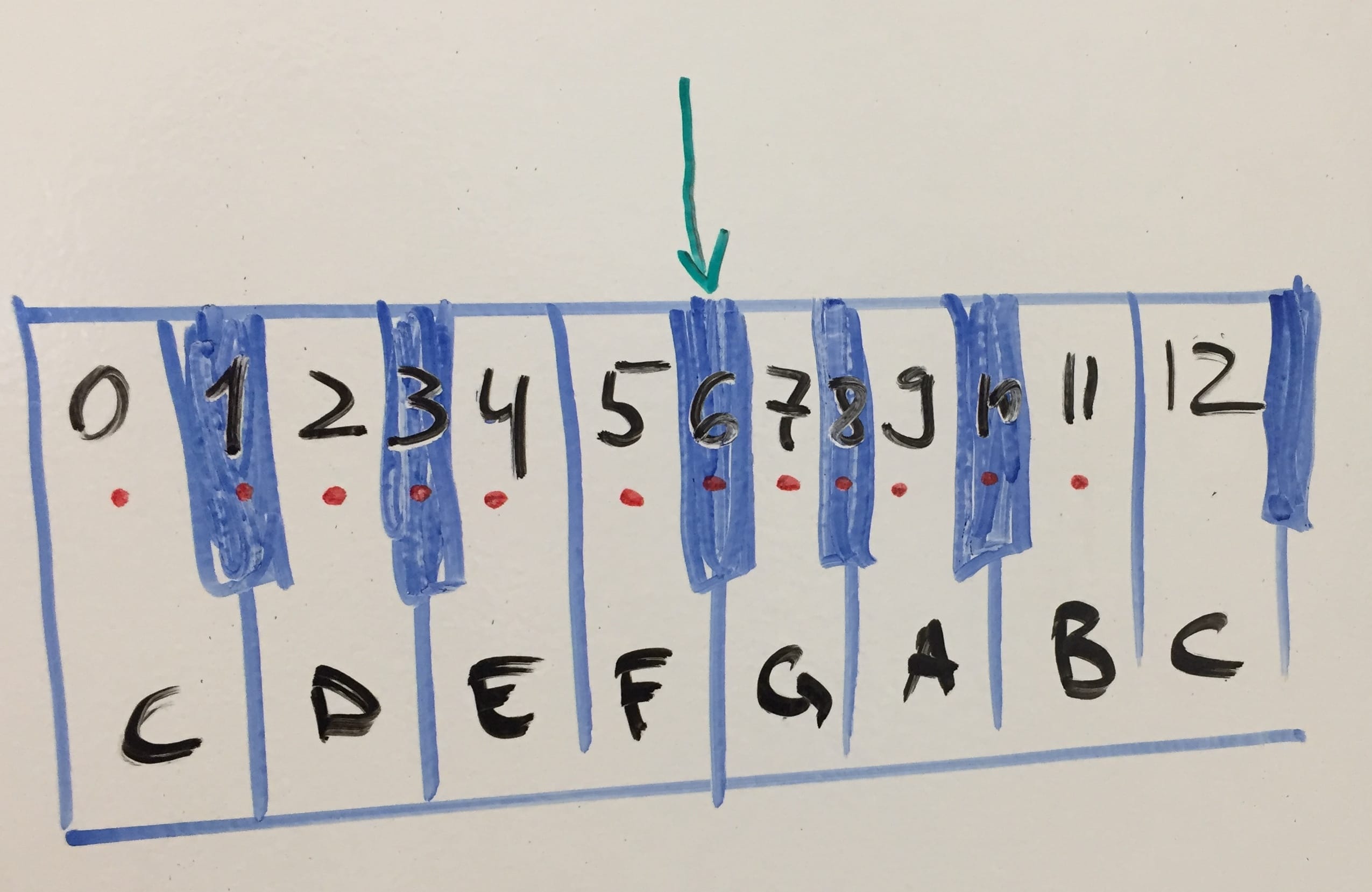
We don’t have a match in the table for 5 lines/spaces and 6 semitones. We have 5 lines and spaces, so it’s a fifth. Only the perfect 7 was diminished by one. How do we call this? You guessed correct – a diminished fifth.
In conclusion, the interval C-G♭ is called diminished fifth.

Let’s add this new information to the table: every time you add 1 to a perfect interval, you call it augmented and every time you subtract 1 you call it diminished.
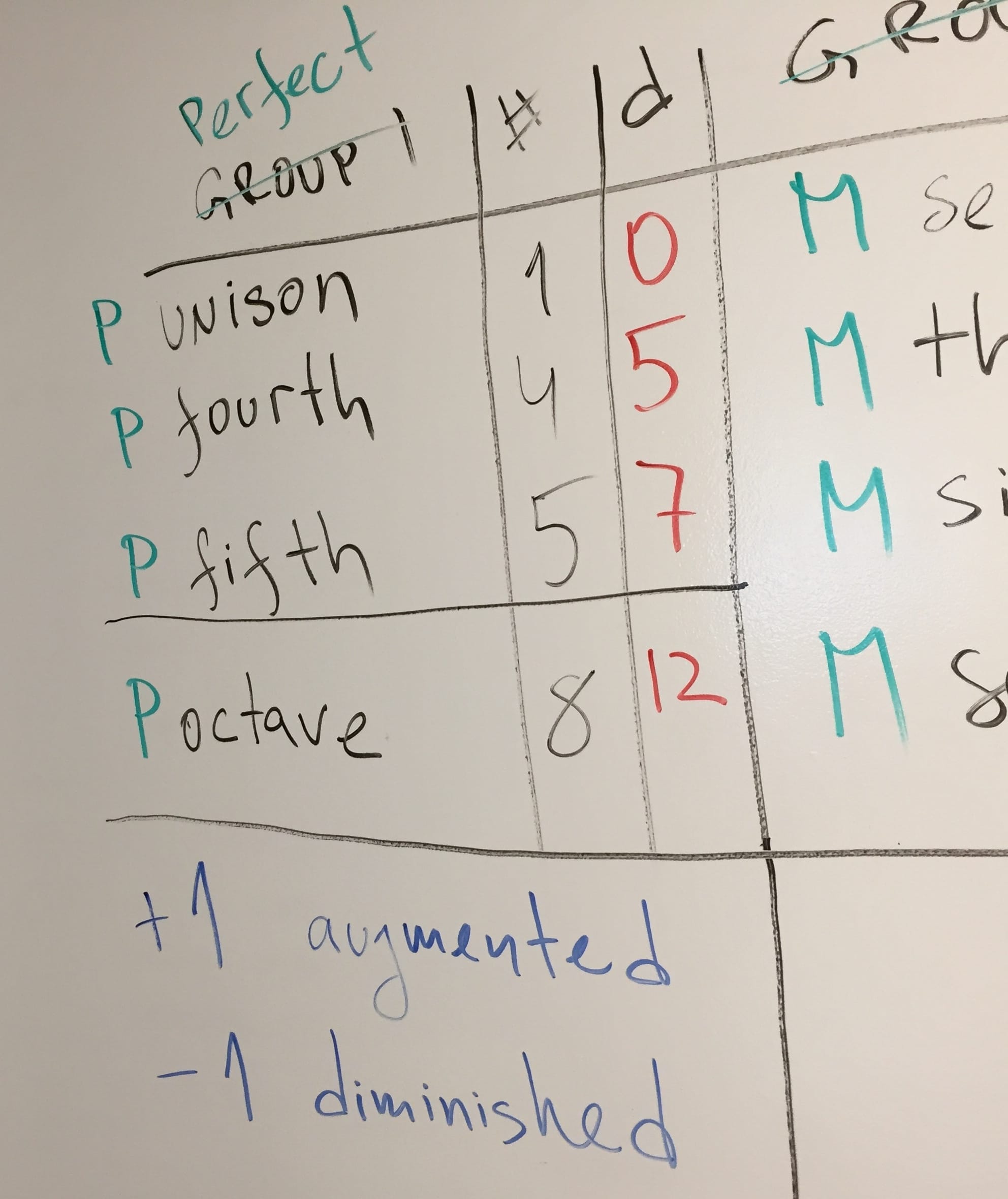
Things are similar, yet a little different, when it comes to the intervals in the second column, the group #2 where the major intervals live.
Adding one still produces an augmented interval. Subtracting 1 is called a minor. Subtracting 2 is now called diminished.

So there you go – the last and final version of the table of intervals. Using this you can figure out any interval there is.

Let’s practice, this time with the major side of the table.
What is this? E to G.

Counting lines and spaces (including the starting point) gives you 3.
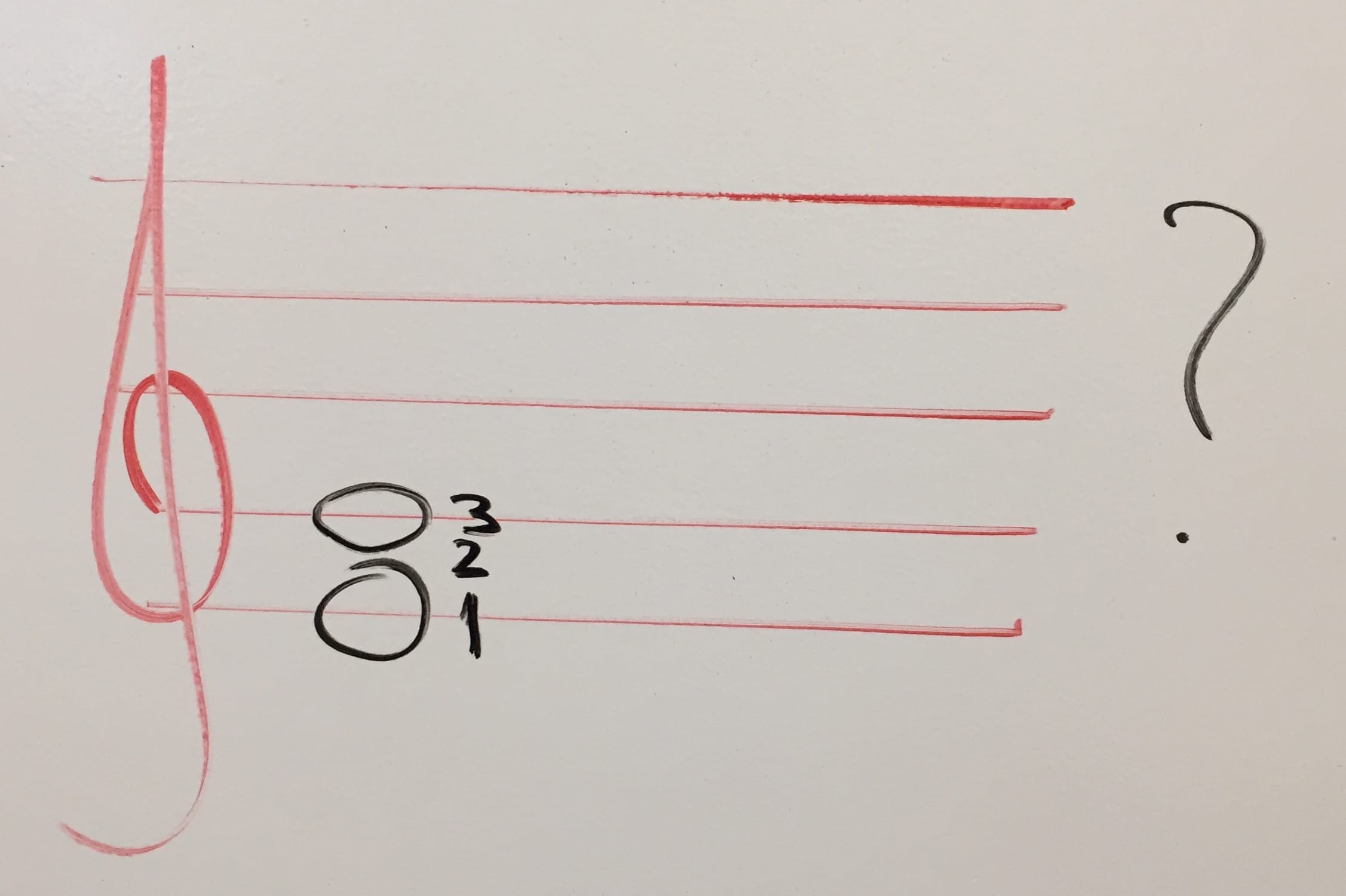
So it’s a third interval.
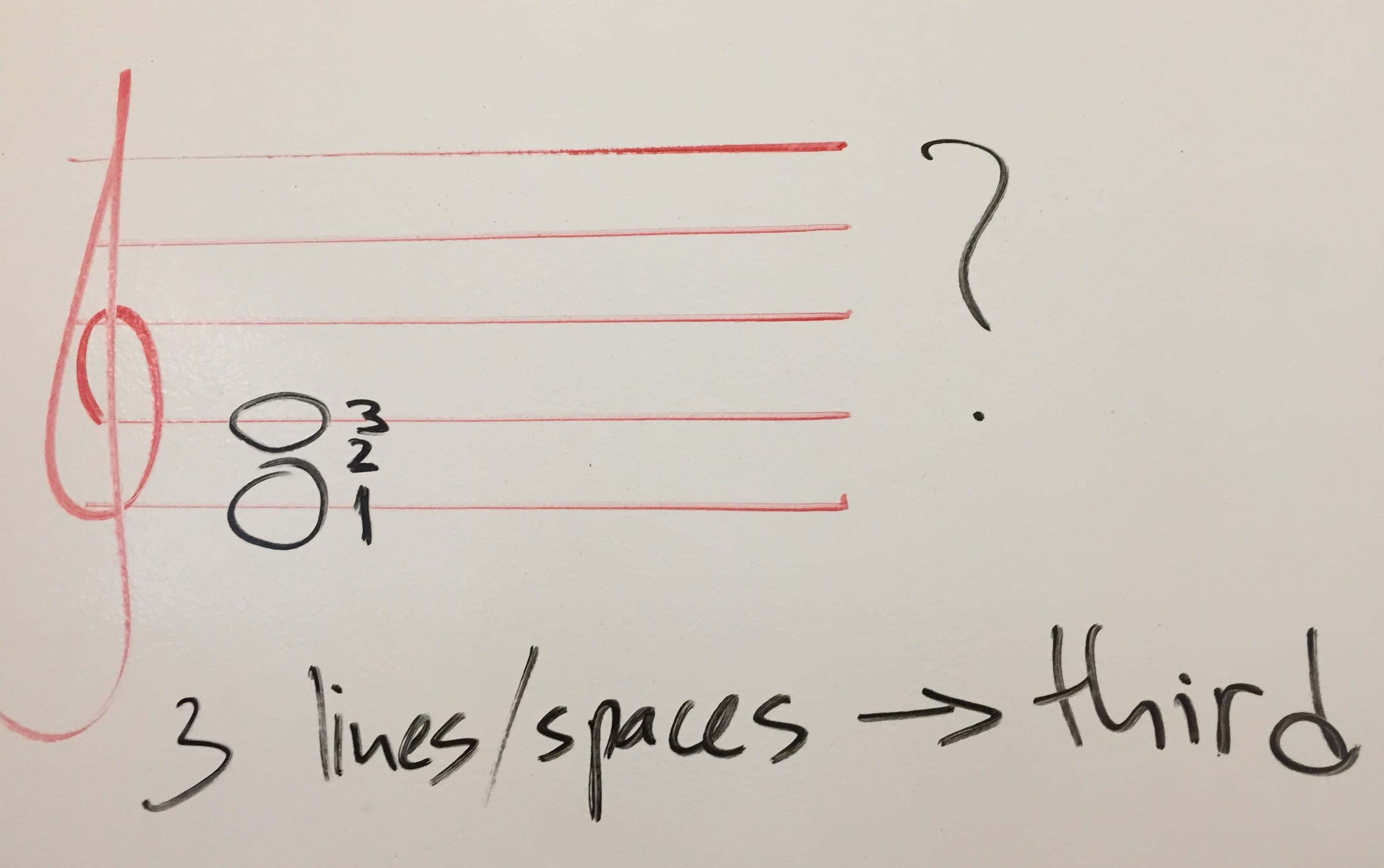
You find the third on the major side of things. It asks for 4 semitones. Is this what we have?

Let’s count on the keyboard. Put a finger on E and count every time you move. F = 1, F♯ = 2, G = 3.
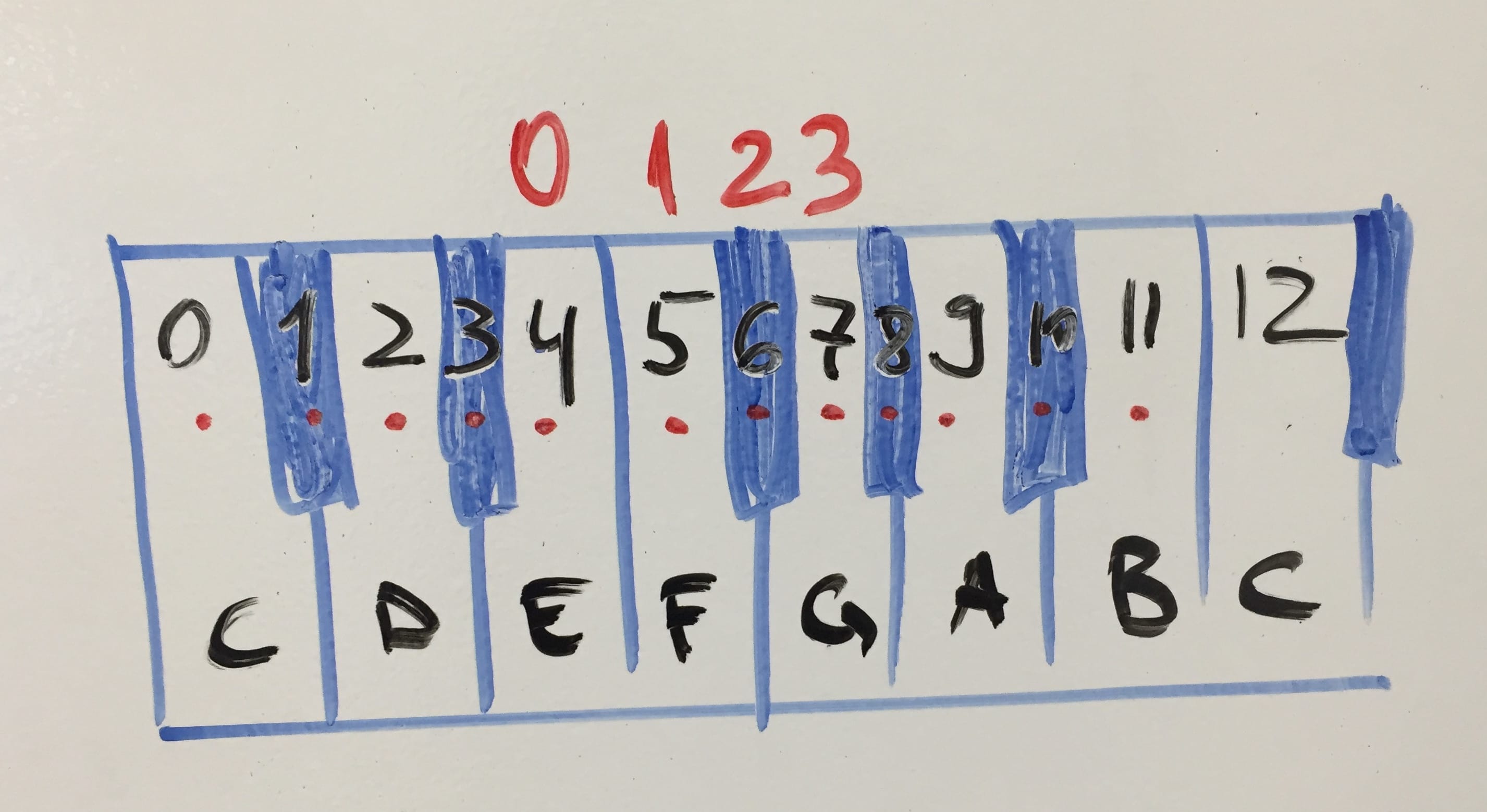
So we counted 3 lines/spaces and 3 semitones.
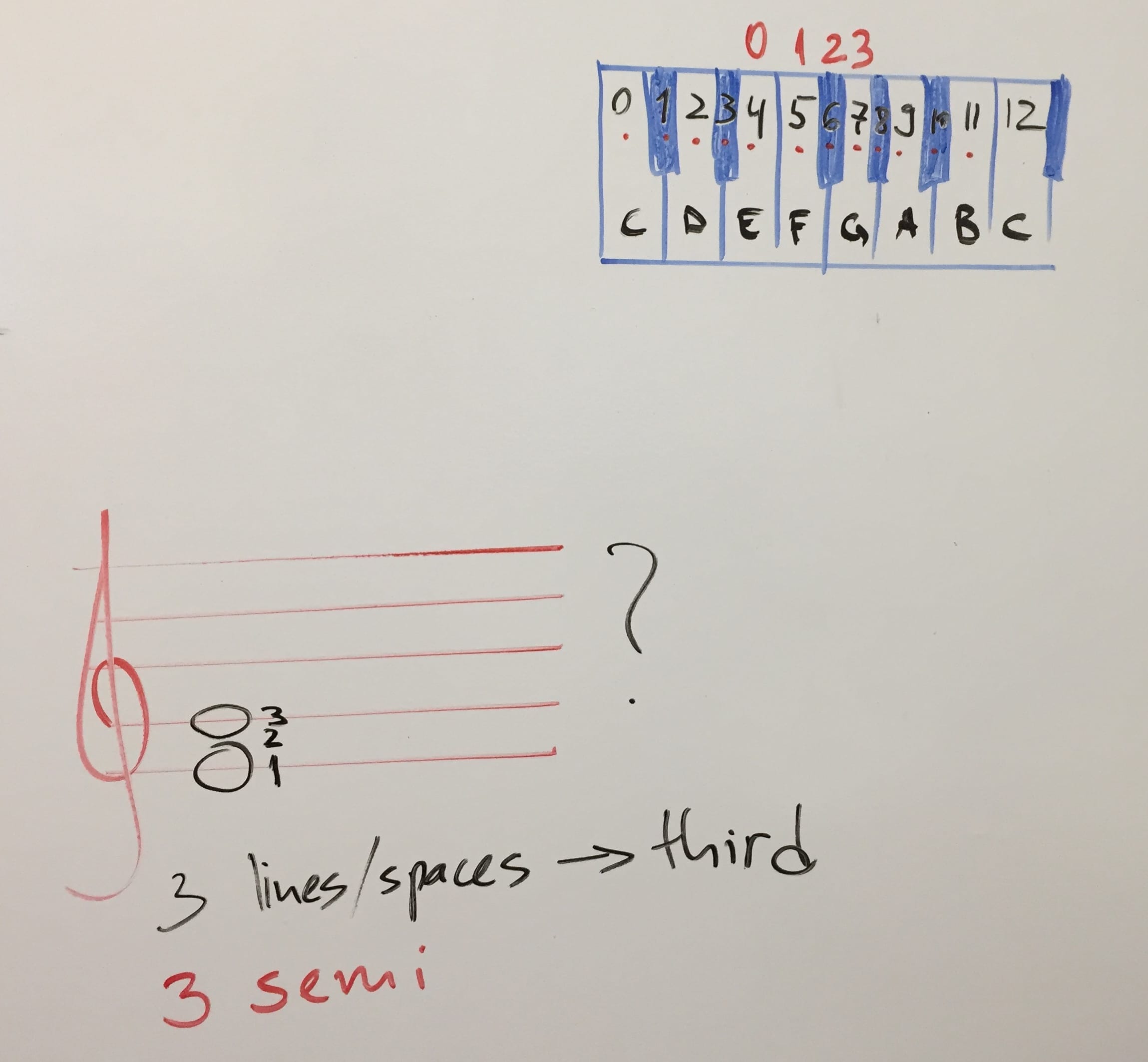
The table asks for 4 semitones. But we have 3.

Looking at the bottom of the table for the short list of corrections.

You need to subtract 1 to get a 3 from a 4. So turns out the interval is minor.

To sum it up, the Answer to the question what is the name of the interval between E and G… it’s a minor third.
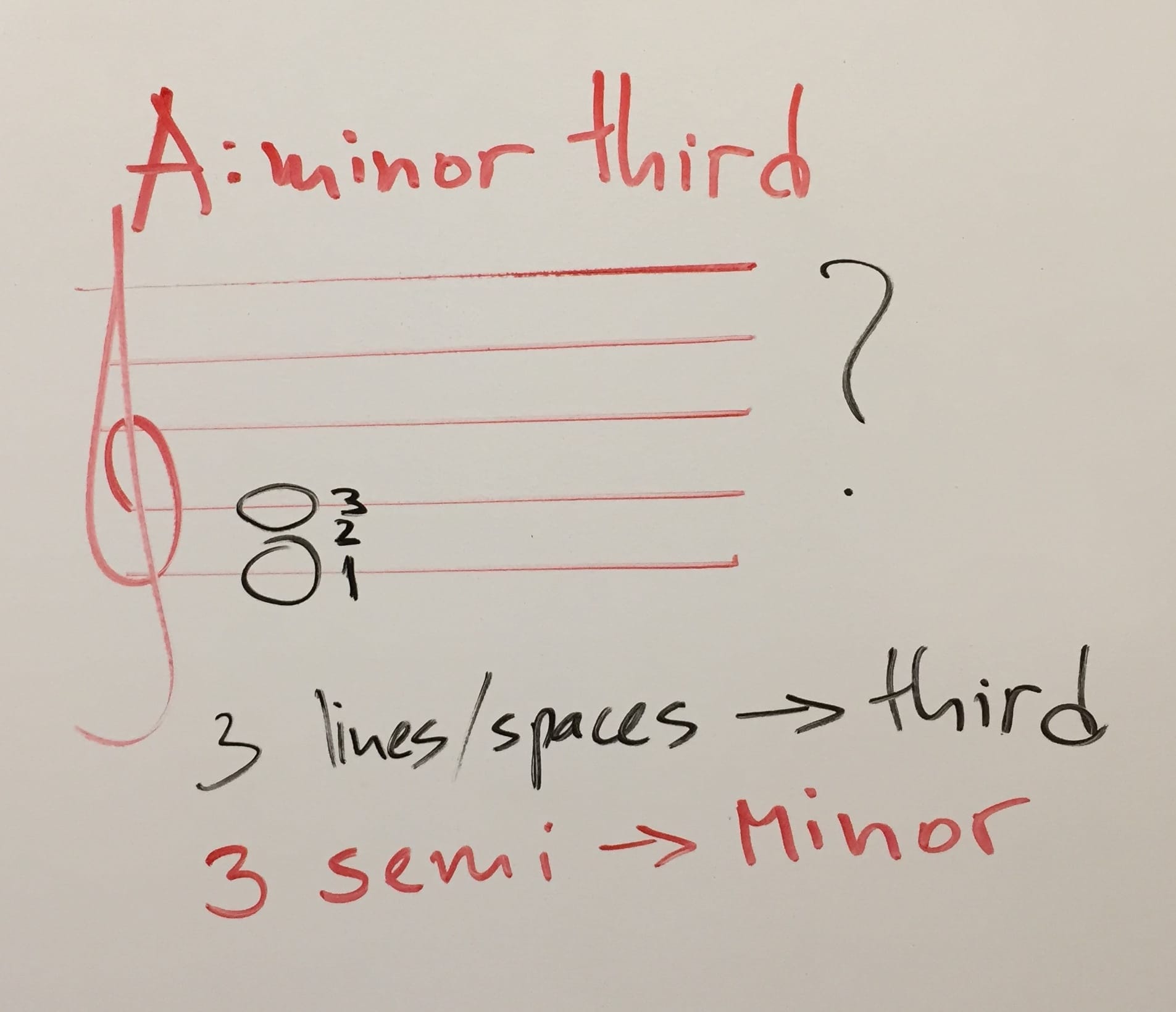
What about E to G♯? It’s still a third (3 lines and spaces on the staff) but with the 4 semitones it matches the number in the major pat of the table. So the interval between E and G♯ is a major third.
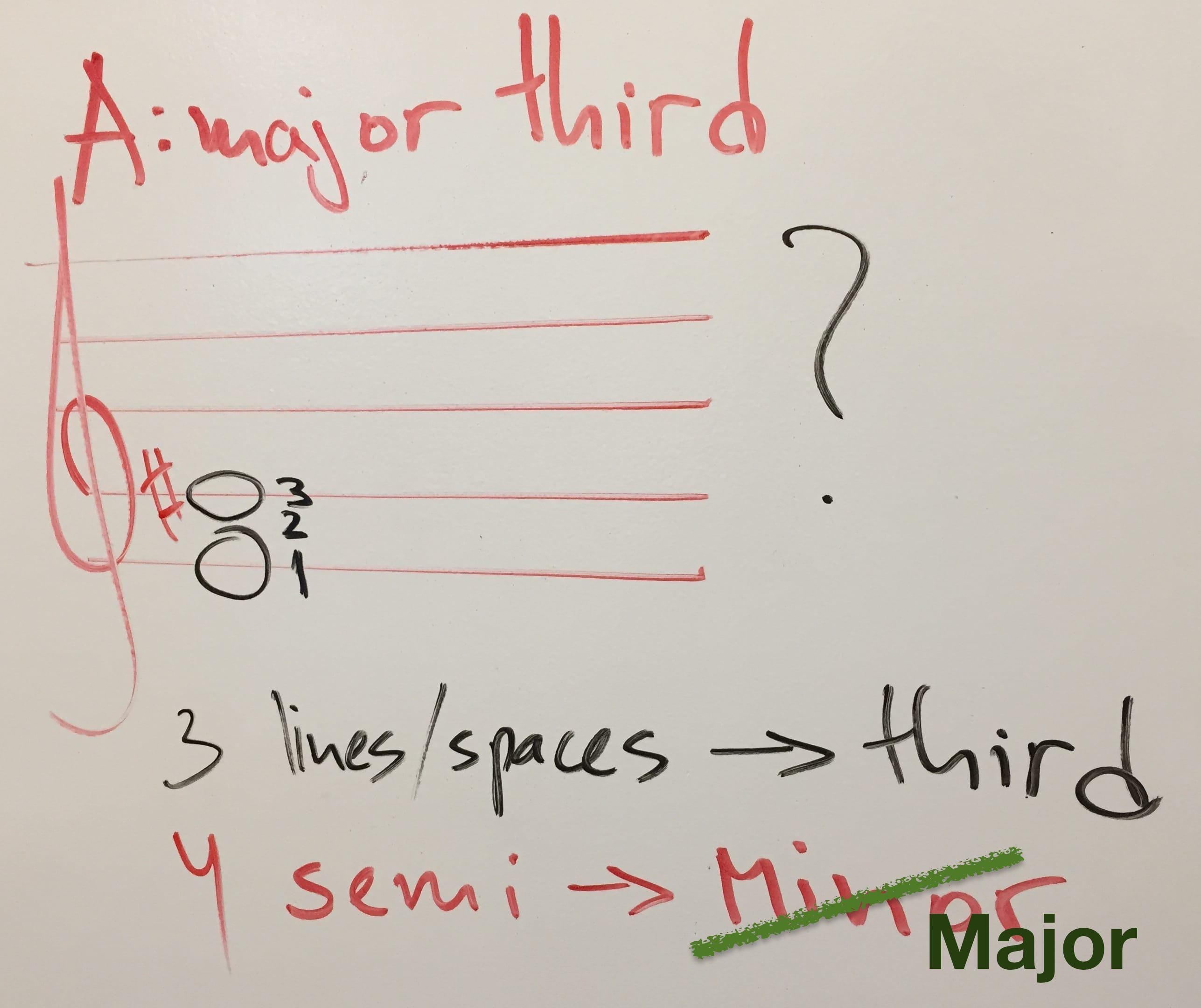
What about the interval E to G♭. Still a third (3 lines/spaces) but with 2 semitones in between (4 – 2 = 2). It’s diminished. All in all the interval E to G♭ is a diminished third.

And what about E to G-double-sharp? Again a third, but with 5 semitones between them (4 + 1 = 5), it’s an augmented third.

And this is how we counted the semitones…
E to G♭… F = 1, F♯ (aka G♭) = 2. Diminished third (because the regular major third asks for 4 semitones and major – 2 = diminished).

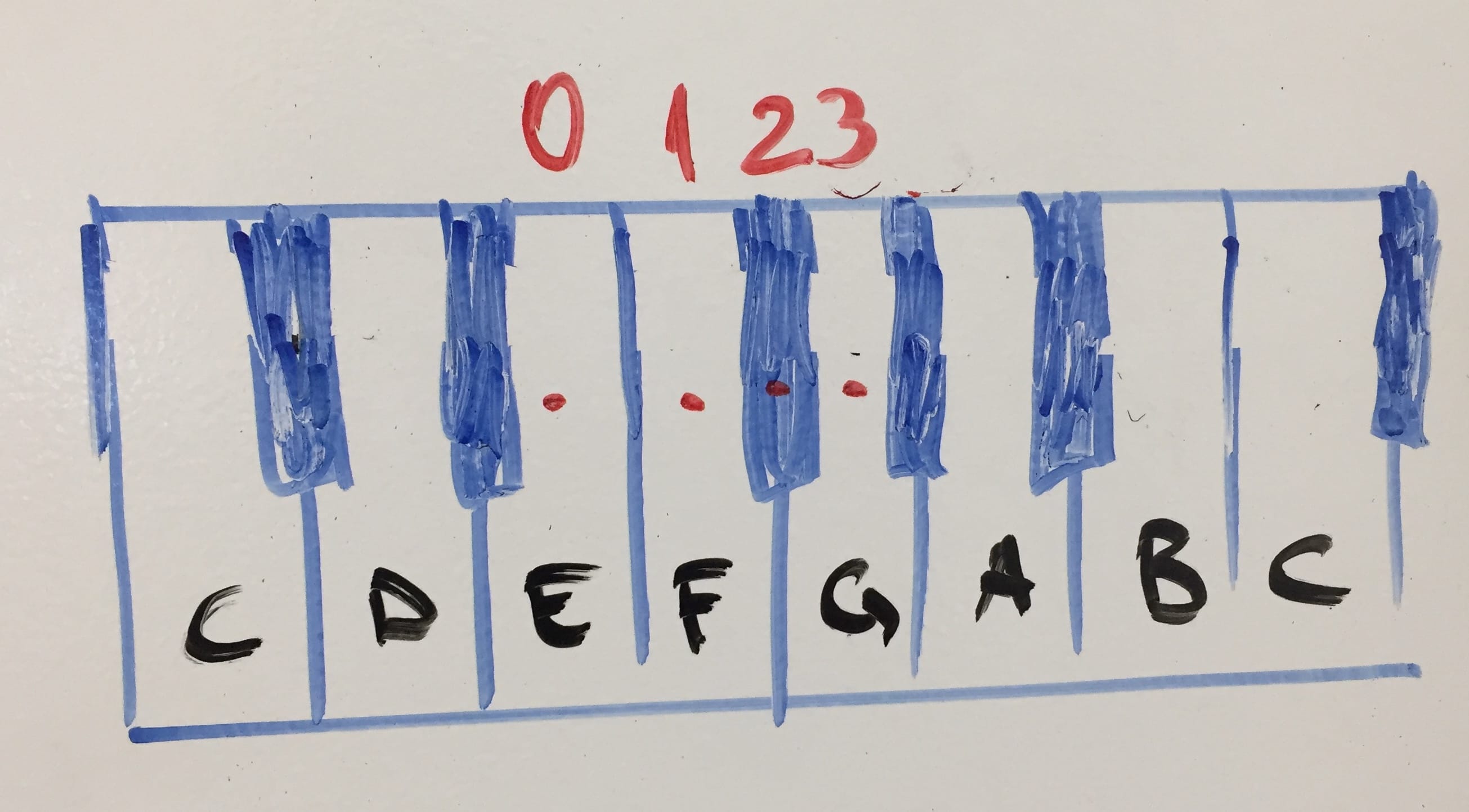
E to G. F = 1, F♯ = 3, G = 3. Minor third. (Major – 1).
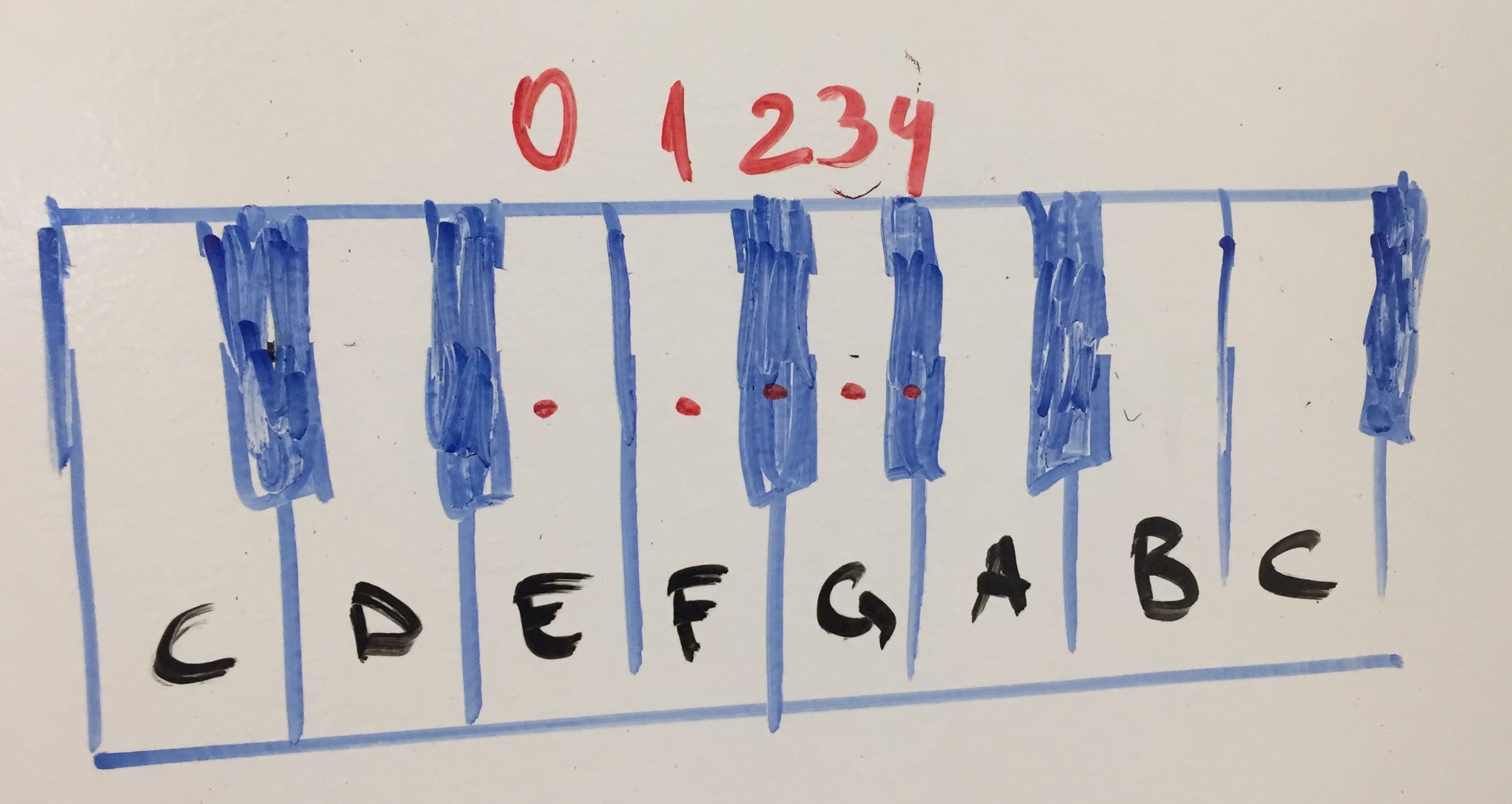
E to G♯. F = 1, F♯ = 2, G = 3, G♯ = 4. Major third (a match in the table)
E to G-double-sharp (Gx is also A). F = 1, F♯ = 2, G = 3. G♯ = 4, A = 5. Augmented third.

Wrapping up
There you have it, ladies and gentlemen. A table of intervals that gives you a way to figure out any interval.

Thank you for reading. Now go practice. Write down a random thing on the staff and go figure it out.
Here’s a start. C to A♭. We did C to G♯ above, and it’s the same sounds. But because it’s written differently, the interval has a different name. What is it?
OK, here’s some more random stuff I put on the staff for you to practice:

OK, now don’t scroll any more, before you’ve done these yourself.
Because I’ll give you the answers.
OK.
Got it?
No more scrolling.
Here come the answers now.
Stop scrolling.
Stop it!
I mean it!
Knock it off!
Enough!
Yo!?!
BTW, If I got any of the answers wrong, please tell me I’m an idiot, publicly on Twitter. (Shaming works miracles!) So I can correct it for the future readers who come across this page 104 years from now. Think of the children.
K, answers:
- fourth, perfect
- fourth, augmented *
- fifth, perfect
- second, major
- second, minor
- fourth, perfect
- fifth, diminished
- third, minor
- fifth, perfect
- fifth, perfect
- third, diminished
- fourth, augmented
- third, diminished
- second, minor
- fourth, perfect
- octave, perfect
* Augmented fourth (or diminished fifth) is the devil’s interval. It was banned by the church at some point as it sound jarring. And how can you blame the ole priest – if you play this interval on an organ in a echoey church, it’s not that pleasant. Nowadays we have our ears more sophisticated, we can appreciate weird stuff like this. Jazz. Blue notes. If played in passing and separately they are cool. If played together as part of a heavy metal composition – hell, yeah! The devil! It’s tricky though. Distorted guitars like perfect fifths. And octaves. Unisons. Maybe, perfect fourths if not too distorted. Playing diminished fifth on a distorted guitar requires them skillz.